Understanding Lie Groups and Manifolds - Foundations of Robotics
This post is still in progress and it only covers the brief of Lie groups.
Lie groups and Lie algebra are fundamental concepts in robotics and one of the trickiest topics, particularly in the field of mobile robotics. These topics can be quite challenging to grasp, but they play a crucial role in understanding how robot movements, specifically rotations and headings, work. In this blog post, we will dive into the basics of Lie groups and their significance in robotics.
The inspiration
My journey into the world of Lie groups began during my time at Northeastern University in Fall 2022. It was in my Mobile Robotics class, led by the esteemed Professor David Rosen, that I was first introduced to the fascinating realm of Lie groups.
The robot navigation problem
To appreciate the importance of Lie groups, let’s start with a simple robot navigation problem. Imagine you have an Inertial Measurement Unit (IMU) that provides you with the heading of the robot. However, this data is accompanied by some level of noise, making it imperfect.
\begin{equation} \theta_1 = 10.1 \end{equation} \begin{equation} \theta_2 = 0.1 \end{equation} \begin{equation} \theta_3 = 0.6 \end{equation} \begin{equation} \theta_4 = 10.7 \end{equation}
These four readings are noisy data, what will be the overall heading of the robot? You might be thinking of averaging the values and you might get the answere as \(\theta = 5.375\). Well this is not the correct answer. Any guesses?
You were asked to estimate the heading of the robot with a noisy IMU data, then why does simple averaging the data doesnot work? Let’s rewind back to high school days of what rotations look like. Rotations look like a unit circle in pure mathematics term it belongs to SO(2) - Unit Circle.
It turns out what averaging the angles gave us belonged to \(\mathbb{R}\) which is a set of real numbers, where as SO(2) is quite a different topology. Having said that rotations belong to SO(2) group and simply averaging them will shift them 180 degrees apart. Look at the figure below.
Now, when it comes to representing and manipulating the robot’s orientation and position, we encounter a challenge. Traditional approaches using standard Euclidean geometry struggle to effectively model and manipulate rotations. This is where Lie groups come to the rescue.
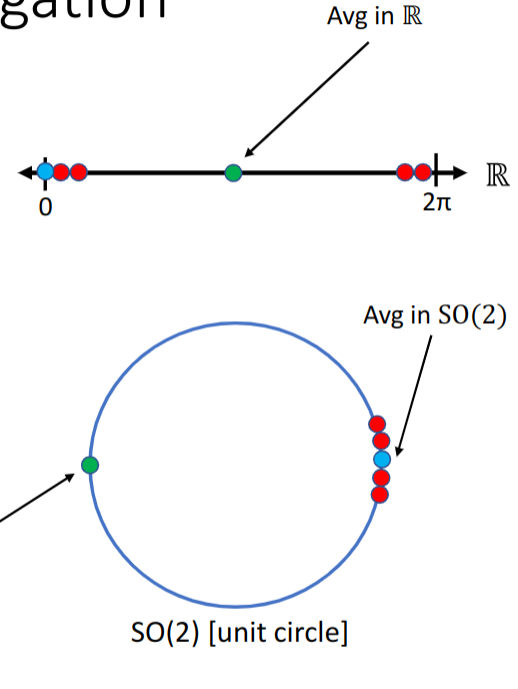
Hence! this says that Rotations are not vectors so you cannot directly take average of them
The need for Manifolds
Similar to this case there are certain cases in robotics where such kinds of vector spaces (euclidean space) are not formed (as they are not preserved under the constraints of addition and multiplication), for instance:
- Rotations as we saw above.
- Viewing headings in Computer Vision
- A set of 2D planes in \(\mathbb{R}^3\) forms a manifold called Grassmanian
Thus Manifolds are used.
The Mathematical Definition of Manifolds
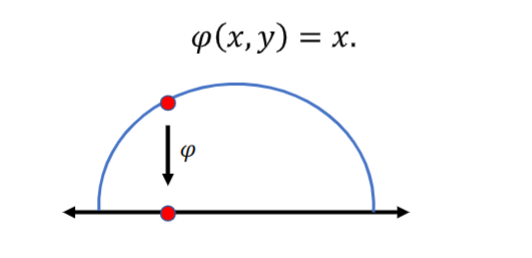
A manifold X is a topological space in which each and every point of this manifold has an open set U and a continous map \(\phi: U \longrightarrow V\) and with a continous inverse \(\phi^-1: V \longrightarrow U\).
Manifolds are spaces that locally look like Euclidean spaces where we can perform our algebraic calculations. A smooth manifold is one whose differentiation exists at every point. A continuous function is one whose differentiation exists but is not guaranteed at each point. We call the tangent space Te(G) the Lie algebra of G. We can think of this as the set of infinitesimal generators for motion on G.
Transition Maps and Manifold Structure
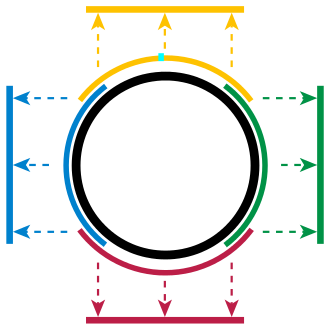
From the below figure X is a smooth manifold if additionally the transition maps \(\phi_{\alpha \beta} = \phi_\beta + \\phi_\alpha^{-1}\) are differentiable in \(\mathbb{R}^n\). For example a transition map that maps the every point of a semi-circle onto a linear axis, and on this linear axis we can perform algebriac steps. Multiple such maps form a unit circle or in other words mulitplw such maps cover an entire manifold.
Now! to the core of this blog,
What are Lie Groups
At their core, Lie groups are a type of mathematical structure that combines the concepts of smooth manifolds and group theory. A Lie group is both a group, meaning it has a binary operation and identity element, and a smooth manifold, meaning it is locally Euclidean. In simple terms, a Lie group is a group with a continuous structure that allows for smooth transformations.
In the context of robotics, Lie groups provide a powerful framework for representing and manipulating orientations, such as rotations and poses. They allow us to perform operations like composition (combining transformations) and inversion (finding the inverse of a transformation) in a seamless and mathematically elegant manner.
Lie groups can be defined as smooth and continuous manifolds that possess a group structure and exhibit smooth and stable motions. They provide a mathematical framework to represent and manipulate rotations, translations, and joint configurations in robotics. In practical terms, Lie groups allow us to smoothly and continuously change joint configurations without causing abrupt or unpredictable changes in the end effector position. This smoothness and stability are essential for precise and reliable robot motions.
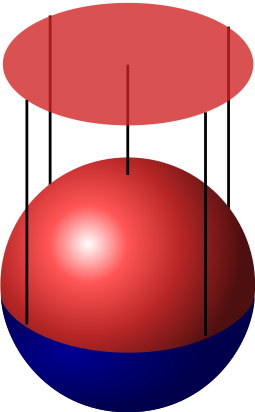
The motion along a Lie group can be expressed as the exponential of rotations and translation matrices, which is known as the exponential map. This mapping allows us to effectively perform calculations and transformations within the Lie group. Furthermore, Lie groups provide intuitive interpretations for certain robot components. For instance, a revolute joint can be seen as a sphere, and the combination of two revolute joints corresponds to taking the Cartesian product of two spheres, resulting in a torus. By leveraging Lie groups, we can develop advanced robotics algorithms, such as motion planning, kinematics, and control, that take advantage of the inherent smoothness and structure of these mathematical objects.
In the upcoming blog posts, we will explore the properties and applications of Lie groups in more depth, uncovering their significance in various aspects of robotics. Stay tuned for a deeper dive into this fascinating topic!
Conclusion
Lie groups and Lie algebra serve as indispensable tools in the field of robotics, enabling us to model and manipulate rotations and poses effectively. Understanding their principles and applications can greatly enhance our ability to navigate the complex world of robotics.
In upcoming post I will talk about the actual implementations of Lie Groups and Lie Algebra of how they are used in robotics and will try to explain it with a real world example.
Thanks for reading ! :)
Dive deeper!
Enjoy Reading This Article? Here are some more articles you might like to read next: